あらゆる測定・計測値に含まれる誤差とその統計的考え方

これまで学んだ計測誤差について本ページにまとめました。自分で勉強した内容をまとめているだけですのでより正確に詳細を知りたい方は計測工学関係の書籍を参照して下さい。本ページでは、高専4年生辺りを読者対象として、特にA/D変換による計測について詳細に書きたいと思います。もし誤りを見つけられましたら、ぜひ教えて頂けると幸いです（連絡先）。
[工事中]

1. 計測と誤差

計測誤差とは、計測値と真値間の差を指します。物・ものを計測して得られた値には本質的に誤差を含みます。例えば、スケールを使って直角ブロックのサイズを計測すると、測るたびに測定値が0.1mm単位で変わるはずです。ノギスで測っても同様に測定ごとに異なるでしょう。また、マイクロメータを使った軸の直径計測でも毎回計測値は異なります^1-1。温度の計測やマルチメータを使用した電圧・電流計測でも同様のことが言えます。さらに、計測者が異なるとその計量値の平均が違う事に気が付くはずです。スケールの見つめ方が異なったり、マイクロメータのねじを締める力が異なったりすることが原因となります。同様にデジタル計測器に表示された数字の丸め方に切り上げやすかったり切り下げやすいなどの測定者の個性が出てしまいます。温度計を同じ仕様の別物に変えたら、示す温度が違ったという事も起こります。

コンピュータの優れた点は、プログラムと実行するコンピュータ及び入力が同じであれば何度計算しても大抵は同じ解が得られることに有ります。ところが、場合によってはアルゴリズムや変数の型・サイズ・演算子の取り扱う有効数字の違いにより誤差を生じます。特に複雑なモデルを構築した場合は、その推定値には確率的な誤差量を与えざるを得ません。

この様に、何を計るにしてもどうしても発生してしまい、必ず検討に入れないといけないのが“誤差”というものです。エンジニアや研究者は科学的に計測値に対して信頼性を与えねばなりません。例えば、「この液体が1度に分泌される体積は95%の確率で23.5±0.3mlだ。」と。

^1-1もっとも、物によっては測定にまごついている間に測定対象が手から伝わった熱で熱膨張を起こしてドンドン計測値が変わるなんてこともあり得ますが・・・。

2. 測定性能の考え方　精度・確度・分解能

科学的に計測誤差を分析する上では精度・確度・分解能と云った概念が重要になります。「精度」とは、普段は何気なく使用しているかもしれませんが、正確には測定値がいかにまとまっているかを示します。例えば、超電導材料を計量する際に何度測り直しても最大0.0001mg（作る量にもよるが）しか差が出ない電子天秤は「精度が高い」と言えます。一方で、この電子天秤は計測値がきっかり2mg多く表示してしまう不具合が有ったとすると「確度が悪い」となります。「確度」とは、計測値が真の値からどれだけ離れているのかを示す指標です。測定器としては、この確度が良い方が良い物となります。ただし、校正手段が用意できるならば確度が悪かったとしても精度さえ良ければ十分使えます（校正作業は大変だが、測定値には信頼性がある）。「分解能」は、どれだけ物を細かく見ることが出来るのかを示す指標です。例えば、私の持っているノギスではバーニアを見ると0.025mm単位で計測できますので、分解能は0.025mmとなります。人用の体重計ならば0.1kg、調理用なら0.1gと言ったところでしょうか。

測定器の性能指標としての分解能は、その計測対象や計測値の運用目的によって大きく要求値が異なります。測定器にはその用途に応じた分解能を求めねばなりません。例えば、ゾウの体重を計測するのにmg単位で計測する必要性はなく、分解能は0.1kgで十分です。なお、分解能が高くとも確度や精度が高くはならないことに注意して下さい。ハードウェア的に無駄に分解能を高めることはデジタル計測ならば簡単に出来てしまいます。温度計測を例に挙げれば、分解能0.001℃で精度95%値で0.5℃なんで直ぐにでも作れますがその高い分解能には全く意味が有りません。

3. 測定値の基本的性質

4. デジタル計測とA/D変換

4.3 A/D変換の精度

A/D変換では、外部や内部要因により必ずノイズが混入します。式4.5をノイズnを考慮に入れた式に書き直すと、式4.5となります。

ADv = ADv₀ + C₀ + n　(4.5)

例えば、H8マイコンやAVRのATmegaシリーズは10ビット分解能の逐次比較型A/Dコンバータを搭載しています。逐次比較型の計測値に含まれるノイズは下2ビットと言われていますので約±3で計測値がぶれる事になります。この様なノイズが含まれていたとしても、周波数解析ではダイナミックレンジが余程小さくなければ問題になりません。ただし、物理量を推定したいときには正確な計測値が分からずに困ってしまいます。より正確な計測値を求める方法が必要です。

デジタル計測に含まれるノイズはホワイトノイズの様に偏りを持たない事がほとんどです。しかも、統計的には図4.1の様に分布する事が分かっています。この分布は正規分布と呼ばれます。分布の特徴としては、センターを境に左右が鏡像になっている事や、平均μ±2σの範囲に約97%の面積が含まれる事が挙げられます。因みに、μ±1.96σの範囲が面積の95%を占めます。

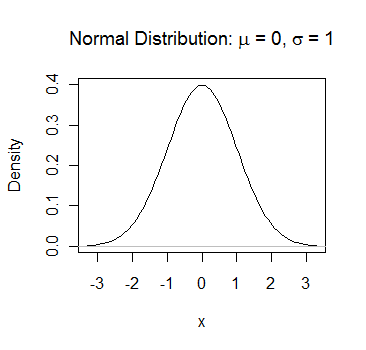
図4.1　ノイズの分布モデル例（正規分布　平均0・標準偏差1.0）
フリーの統計処理ソフトRを用いて描画した。

A/D変換の測定精度を求める例を以下に示します。 Arduino (MCU CORE is ATmega328.)を用いてA/D変換を行いました。 A/D変換にはA0ポートを使い、プログラムはArduino IDEのA/D変換サンプルプログラムを用いました。観測の様子を図4.2に示します。 A0ポートと3.3V出力端子間に10kΩの炭素被膜抵抗を入れて計測しました。 AVrefは、電源電圧がそのままA/D変換の基準電圧に使われていますので5Vです。入力が3.3Vですので理想A/D変換値は式4.2を用いて675.18となります。なお、計測値に適当なノイズが混入すれば、その平均値はADv₀ + C₀に近づくことが期待されます。この事は式4.5において、十分に多くのサンプルを平均すればノイズ項nは0となる（ノイズの平均は0）事で分かります。レギュレータの出力誤差（最大2%程度）を考慮に入れれば、ADv₀ + C₀は最悪の場合で約650～700となります。

(a)

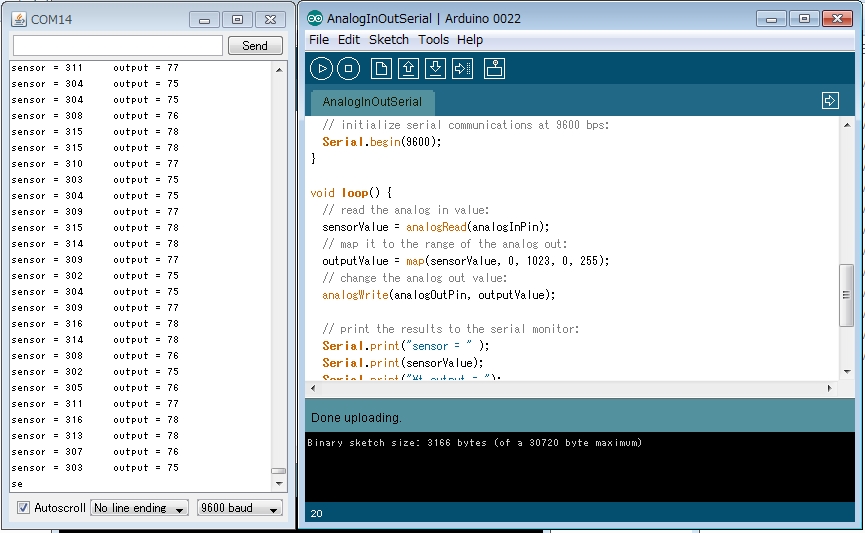
(b)

図4.2　Arduinoを用いたA/D変換の様子
データ収集にはArduino開発環境であるarduinoに標準で搭載されているA/D変換サンプルプログラムを利用した。シリアルの通信記録にはtera termを用いた。

図4.3に計測値のヒストグラムを示します。ほぼ予想通りに分布している事が分かります。予想値である675.18との差がC₀かどうかは、入力電圧・基準電圧を計測してその影響を評価しなければ分かりません。

という訳でAVrefとVinを計測してみると、それぞれ5.02 Vと3.33 Vであることが分かりました（有効数字の少ない計測器ですみません）。この値を用いて再計算すると、ADv₀ = 679となります。従って、計測結果にはC₀はほとんど含まれていなかったと言えるでしょう。ただし、ヒストグラムの左右がシンメトリになっていないのは何度測っても同じでしたからこれがAD変換器に起因する誤差だと言えます。なおArduinoの場合、AVrefの計測はA/D変換の実施中に行うようにして下さい。電源ラインが貧弱ですので負荷変動に伴い基準電圧が変わってしまいます…。

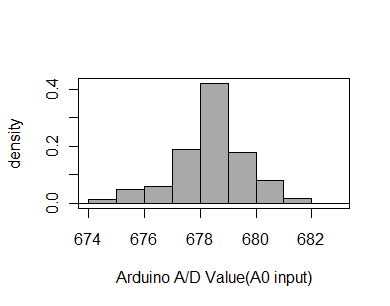
図4.3　A/D変換の結果得られた計測値のヒストグラム

表4.1に計測値の数値的要約を示します。平均に加えて、A/D変換には時折大きなノイズが混入する事があるため参考のために、中央値を含む4分位数も示しています。この実験では、平均と中央値に大きな差はありませんでした。 μ = 678.9, σ = 1.295ですので、観測値が正規分布に従うならば678.9 - 1.96 * 1.295< ADv <678.9 + 1.96 * 1.295（μ±1.96σ）の範囲に95%の観測値が含まれる事になります。含まれている様に見えますでしょうか？

表4.1　計測値の数値的要約

平均	標準偏差	4分位　0%	4分位　25%	4分位　50%	4分位　75%	4分位　100%	サンプル数
678.888	1.295	674	678	679	680	683	8598

参考に、実験データを基に平均678.9，標準偏差1.295の正規分布図を図4.4に示します。分解能が十分に大きければこの様な分布になったと考えられます。

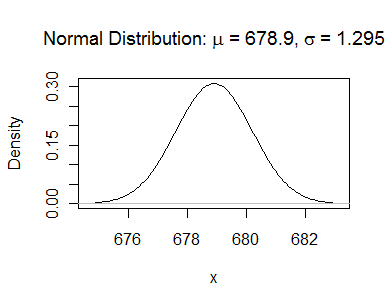
図4.4　平均678.9，標準偏差1.295の正規分布図

以上の例における計測精度は、95%で±2.54であると言えます。言い換えると、真値は計測値ADv±2.54の範囲内である確率が95%という事です。

蛇足ですが、正確な観測値を知りたい場合、計測値を降順に並び変えて最大最小に近い数サンプルを捨てた上で平均を取る様にして下さい。 Nサンプルの平均で分解能が√N bit増えるとされています。単に移動平均を施した場合の結果を図4.5に示します。これはArduino IDEのAnalog-Smoothingサンプルを利用しています。平均は678.9となり、標準偏差は0.58となりました。明らかに計測精度が向上したことが分かります。母集団がどの様な分布をしていようと、そのサンプルの平均をいくつも取ると正規分布となることを利用して更に精度を高めることも出来ます。ただし、時間分解能が落ちることに気を付けて下さい。

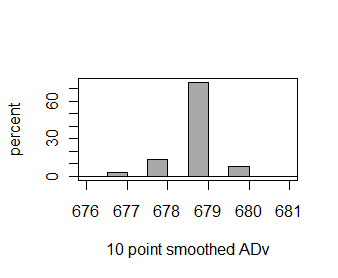
図4.5　10ポイントの移動平均結果　

5. おまけ　計測値の扱い方

5.2 A/D変換値から物理量を求める

プログラムのアルゴリズムによって分解能が下がる例を示します。

式(4.2)を変形すれば入力電圧を計測することが出来ます。首尾よく入力電圧が分かれば、それをセンサのデータシートから読み取った出力電圧－物理量関係式へ入力して物理量を求められます^5.2-1。とろろが、初心者は入力電圧を求める段階で分解能を落としてしまうことが有りがちです。紙面上で計算する様にはプログラムは動作しないという認識が足りないことが直接の原因です。精度を保ったまま計算を行うためには、変数の型と演算規則に注意を払いつつ数式を立てねばなりません。

以下に、AD変換の分解能が10ビットだったときのプログラム例を示します。ここで、下記のプログラム例ではint型のAD変換結果を返す(int)get_ADv(void)を呼び出しています。この関数は呼び出すと自動的にAD変換を実施し、その結果を返すものとします。入力された電圧を計測した後に、物理量（例えば温度）に変換しています。

			/****************************
			* 電圧をまず求める。
			* 基準電圧は5.0Vとする。
			* C言語の例です。
			* int:16bit, long:32bit
			*****************************/
			int v_in, temp;
			
			v_in = get_ADv() * 5 / 1023; // (5.1) 入力電圧を計算する。
			temp = 37 * v_in - 51;       // (5.2) 物理量に換算する。

図5.1　物理量を求める計算の失敗例　その1

ここで、式(5.2)がセンサの特性である出力電圧－温度換算式を表しています。これはノートに書いた数式と同じ形をしています。式(5.1)は式(4.2)を変形して求めた入力電圧を求める式です。一見正しく動きそうですね？このプログラムを動かすとどのような結果になると思いますか？答えは、「上手く動かない」です。原因を探るためにv_inを調べてみると、0,1,2,3,4,5という非常に粗い離散値しかとらないことに気が付くはずです。このままでは、tempは-51,-14,23,60,97,154という離散値しか取り得ません。これは整数演算は小数点以下が切り捨てられるというプログラミング上の基本的規約によるものです。プログラマーがこの様な単純ミスを犯してしまう原因は、変数型というプログラミングの初歩についての知識がないことにあります。単純で初歩的な事ですが、学校の授業を受けただけでは全く身につかない困った原因です。ちなみに、式(5.1)をv_in = get_ADv() / 1023 * 5;と書いてしまうと最悪です。 *と/は演算子の優先度が同じであるため、式は左から処理されてしまい、最終的に答えは常に0となります。

では、どうすればもっと細かく温度を計算することができるのでしょうか？そのためには図5.2の様にプログラムを訂正します。式(5.3)を見ると、先ほどの計算値よりも10倍されていることが分かります。さらに式(5.4)では51の10倍である510を引いて最後に全体を10で割っています。こうすると入力電圧は0.0～5.0の有効数字2桁で処理されるため、温度も概ね有効数字2桁で計算されます。温度の値は、今度は-51,-47,-43,…となります。ところで、普通はここで第2の壁にぶつかるはずです。それはget_ADv()の返す値が656以上となると値がおかしくなるかCPUが暴走するという問題です。いずれにせよマイコンは突然正常な動作をしなくなります。

			/****************************
			* 電圧をまず求める。
			* 基準電圧は5.0Vとする。
			* C言語の例です。
			* int:16bit, long:32bit
			*****************************/
			int v_in, temp;
			
			v_in = get_ADv() * 50 / 1023;         // (5.3) 入力電圧を計算する。
			temp = (37 * v_in - 510) / 10;        // (5.4) 物理量に換算する。{37 * v_in / 10 - 51}としては意味がない。

図5.2　物理量を求める計算の失敗例　その2

上記の原因はint型変数が扱える最大値を演算途中で超えたことです。演算の結果を格納できるだけの大きさが変数に求められます。図5.2のプログラムを改善したものを以下に示します。

			/****************************
			* 電圧をまず求める。
			* 基準電圧は5.0Vとする。
			* C言語の例です。
			* int:16bit, long:32bit
			*****************************/
			long int v_in, temp;
			
			v_in = (long int)get_ADv() * 50l / 1023l; // (5.5) 入力電圧を計算する。
			temp = (37l * v_in - 510l) / 10l;         // (5.6) 物理量に換算する。

図5.3　物理量を求める計算の成功例

気が付いたでしょうか？変数がlong int型となり、演算がすべて32ビットで行われるようになっています。一貫してlong型で計算するためにリテラルデータ（37や510などの実数）にはlを後ろに付けています。これで正常に温度を求めることができるようになりました。しかし、このAD変換器の分解能は約5mVなのに計算上100mV単位でしか扱わないとはもったいない話ですね？分解能を上げたコードを図5.4に示します。

			/****************************
			* 電圧をまず求める。
			* 基準電圧は5.0Vとする。
			* C言語の例です。
			* int:16bit, long:32bit
			*****************************/
			long int v_in, temp;
			
			v_in = (long int)get_ADv() * 500l / 1023l; // (5.7) 入力電圧を計算する。
			temp = (374l * v_in - 51200l) / 100l;      // (5.8) 物理量に換算する。{(374l * v_in - 51200l) / 1000l}としては意味がない。

図5.4　物理量を求める計算の分解能を挙げた例

式(5.7)では入力電圧が0.00～5.00Vまで計算できますので分解能は約10mVとなりました。従って入力電圧の有効桁数は3桁になっています。折角入力電圧の分解能が3桁に上がったのですから温度の計算値も3桁に上げました。図5.4によって得られるtempの値は-512,-508,-504,-500,…となります。これは、温度が-51.2,-50.8,-50.4,-50.0,…となることを示しています。つまり、式(5.8)では温度が15.2℃ならばtempが152となります。

この節で取り上げた様に、ハードウェア制御には数値演算の力がなければ上手く行きません。予め微分方程式を解くなどの数値演算を経験していれば、ハードウェア制御もスムーズです。

^5.2-1A/D変換値－物理量関係式を求めるとより高精度に計算できます。